Ángulos y giros

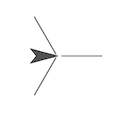
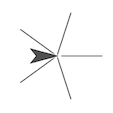
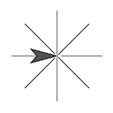
En esta página vas a aprender sobre ángulos, elementos necesarios para dibujar polígonos. Para principiar, se dibujan asteriscos similares a los siguientes:
three-spokes five-spokes eight spokes

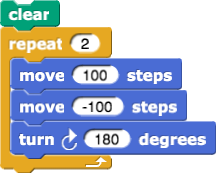
En el ejercicio anterior se buscaba dibujar un triángulo equilatero, un posible código es el siguiente:

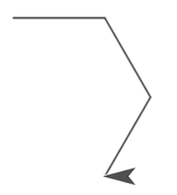
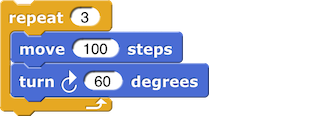Brian, these images need alt/title text. --MF, 9/1/19
y presenta el siguiente resultado:
Es común intentar dicha aproximación, ya que se sabe que los ángulos de un triángulo equilateral tienen todos 60 grados. Sin embargo, él cursor debe girar 120 grados, y es importante entender la razón y la forma correcta para definir los ángulos de otros polígonos (cinco lados, siete lados, etc.).

  1. Click here to load this file for the first set of experiments. Then save it to your Snap! account.
  2. Ejecuta los cuatro experimentos (A-D) y lee los comentarios asociados a cada uno. Mientras se realiza el experimento debes conversar con tu compañero el resultado y su respectiva explicación.
  3. Luego, experimenta con el último ejercicio (D) (se muestra a la derecha):
    repeat (2): {move (100) steps, move (-100) steps, turn (180) degrees}
    1. Experimenta con un cuarto de vuelta (gira 90 grados en lugar de 180). Ajusta el número de repeticiones (es el número que se proporciona al bloque repetir) hasta que se logre llevar al cursor a la misma posición en la que empezó.
      Angle Experiment with 4 turns.
    2. Experimenta con una décima parte del giro (giro a 36 grados). ¿Qué valor se debe asignar al bloque repetir para lograr que el cursor finalice orientado en la misma forma en que empezó?
    3. Si intentarlo aún en la computadora, piensa el ángulo de giro para dibujar un asterisco de cinco puntas. Asegúrate de razonarlo con tu pareja.
    4. Luego, prueba el experimento.
  4. Talk with Your Partner Describe que has aprendido acerca de ángulos de giro.
  5. Al inicio del ejercicio se conversaba sobre triángulos. Para seguir en esa dirección, dibuja un asterisco con tres puntas.
    Haz clic para obtener una pista.
    image of three spoke asterisk being drawn slowly with the sprite tracing out a different color in each third
Un giro de 360° representa una vuelta completa. La mitad de eso (180°) es una media vuelta. Un cuarto de 360° 360-divided-by-4-with-result-90 es un giro de noventa grados. No es necesario hacer la división en cada oportunidad, ya que Snap! tiene una función para ello. Se puede utilizar el bloque turn-360-divided-by-7-degrees o el bloque turn-360-divided-by-3-degrees para una séptima parte de una vuelta, o un tercio de giro.
Pair Programming Swap

En el inicio del ejercicio ya conocías la forma de hacer un triángulo por medio de giros de 120 grados, aunque posiblemente no sabías la razón. Ahora ya sabes que el ejercicio de crear un asterisco de tres puntas necesita giros de 120°, ¿pero cuál es la relación de los giros de 120 grados con los triángulos?

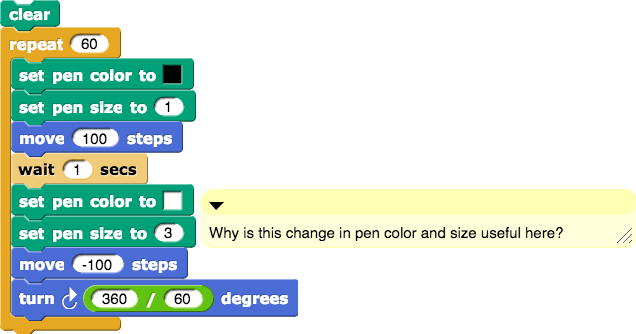
  1. Prueba diferentes valores negativos dentro del bloque move -100 steps (de primero prueba con -90, luego -50, luego -10), y realiza más experimentos con cada valor. ¿Estos cambios afectan en los valores que se necesitan para los bloques repeat o turn? Estas imágenes se llaman "molinillos."
  2. Click here to load this file for the second set of experiments. Then save it to your Snap! account.
    Ahora ejecuta el ejercicio (A) y experimenta con los siguientes valores:
    1. Cambia los valores del ejercicio A para dibujar el asterisco con:
      1. 5 ramas
      2. 8 ramas
      3. 3 ramas
    2. Haz una copia del programa para dibujar un asterisco con tres ramas (clic-derecho o control-clic en el programa, y elige "duplicar").
      1. En la copia remueve el bloque move -100 steps.
      2. ¿Qué hace el nuevo código?
    3. Haz una nueva copia del programa para dibujar un asterisco con tres ramas, luego:
      1. Cámbialo para que dibuje cuatro ramas.
      2. Remueve el bloque move -100 steps.
      3. ¿Qué hace este nuevo código?

Depurando con el bloque say for

Es posible usar el bloque say for para obtener información acerca de el estado del programa que se encuentra en ejecución. La siguiente animación muestra la forma de usar el bloque say for para entender el posible error en un código con problemas para dibujar un rectángulo. Toma nota de la forma en que el programa hace una pausa y proporciona información útil para ayudarte a identificar la posible fuente del error.

Animation on how to use say for blocks for debugging an erroneous rectangle construction.
  1. El ejercicio B en el archivo descargado muestra la forma de hacer que un asterisco de 60 ramas se comporte similar a la segundera de un reloj. ¡Pruébalo!
    • Talk with Your PartnerAsegúrate que eres capaz de explicar cómo este programa hace lo que ves en pantalla.
    • ¿Porqué es importante cambiar el color del lápiz y su tamaño en esta parte del ejercicio?
      clear;repeat(60){set pen color to (black); set pensize to (1); move (100) steps; wait (1) secs; set pen color to (white); set pensize to (3); move (-100) steps; turn clockwise(360/60) degrees}
                    
Alma Thomas
  1. A la derecha se presenta una pintura de Alma Thomas. ¿Te insipira a dibujar tu propio trabajo?.
    Es tu inspiración. Sé libre para expresarte.
    Gamal: Me parece la figura de un mapa. Veo casas a la derecha, el centro de la ciudad a la derecha. Veo la municipalidad, estación de bomberos y un supermercado.
    Betty: Probablemente. A mi me parece que la izquierda representa las huellas dactilares. Por otra parte la sección a la derecha representa claramente una persona con su mirada hacia la derecha, con su nariz hacia arriba.
    Alphie: No importa mucho a qué parece la pintura. ¿Cómo vamos nosotros a lograr que nuestro trabajo luzca parecido?
    Betty: Partes de la pintura tienen un aspecto curvo, líneas punteadas gruesas. Podemos hacer algo como lo siguiente:
         
    Aunque no estoy segura cómo generarlos en gran cantidad y lograr que esten acomodados juntos.
    Alphie: La aleatoriedad es nuestra amiga. Hagamos muchas líneas punteadas, de diferente grosor y que apunten en diferentes direcciones.
         
    Betty: Wow! Es una muy buena idea.
    Alphie: Aunque el resultado no es lo que tenía en mente para el ejercicio.
    Betty: ¿A qué te refieres? Recuerda la primera instrucción que se encuentra en negrillas al inicio del ejercicio.
    Alphie: Sí, lo tengo presente, pero la frase "Sé libre" no significa "Sé feliz con el resultado que salga en el primer intento." Yo tengo otra idea. Hemos estado pensando en la pintura de "Thomas" en la forma de cuadros de color café sobre un fondo blanco, aunque es realmente más café que blanco. ¿Qué tal si empezamos con un fondo café y dibujamos líneas blancas sobre él?
    Gamal: ¿Qué sucede con el centro de la ciudad a la derecha?
    Betty: Esto no es un mapa. Pero para hacerte feliz, en el momento de dibujar las lineas blancas hacia la derecha, pueden ser más gruesas. De esta forma la parte derecha tendrá más espacio en blanco que la parte izquierda.
    Alphie: Uh oh... Si ves detenidamente la pintura original, puedes notar que los elementos en color café no tienen todos la misma tonalidad.
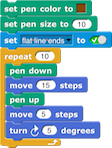
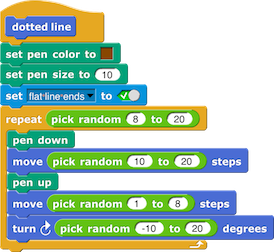
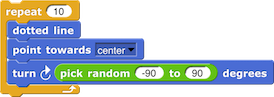
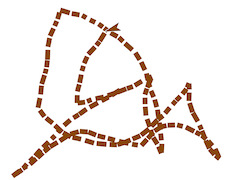
    Betty: Alphie, te preocupas demasiado. Pero para hacerte feliz de nuevo, una vez que tengamos el espacio dividido en regiones, podemos usar el bloque para rellenarlas en varias tonalidades de color café.
    Gamal: Hey! Amigos! ¿Recuerdan que importamos la biblioteca de crayones? ¿Adivinen qué? Tenemos una biblioteca "Mapamundi", también! Dicha bibloteca dibuja mapas "watercolor" que se ven de la siguiente forma:

    Luego recorrí cada uno de los puntos del escenario utilizando los bloques y para decidir entre hacer el punto blanco o café:
  2. ¿Cuál era la idea original de Alma Thomas al realizar su pintura: un mapa, una huella dactilar, o algo más? Investiga un poco.